Wie sich die RDC-Performance im Antriebsstrang simulieren lässt

Wie lässt sich die Performance eines Resolver-Digital-Wandlern (RDC) in einem Antriebsstrang simulieren? Und wie können reale Ereignisse – wie etwa ein starkes Bremsen oder plötzliches Beschleunigen des Fahrzeugs – analysiert werden?

Anbieter zum Thema

Metrofunk Kabel-Union GmbH

Die verschiedenen Subsysteme eines Autos stellen vielfältige Anforderungen. Zum Beispiel können an der per Keilriemen angetriebenen Generator-Anlasser-Kombination Beschleunigungen bis zu 50.000-1/s auftreten, während sich die Beschleunigung von per Kurbelwelle angetriebenen Systemen im Bereich von 20.000-1/s bewegt. Bei industriellen Anwendungen können sehr dynamische Servomotoren in zwei bis drei Millisekunden von null auf eine Drehzahl von 5.000-1 beschleunigen.

In bestimmten Anwendungen sind starke Bremsungen und sofortige Beschleunigungen möglich, wenn der Motor wegen eines Hindernisses angehalten wird. In solchen Einsatzfällen kann es zu Verzögerungen und Beschleunigungen von bis zu 200.000 rad/s² kommen. Unter diesen Umständen werden kurzzeitig größere Positionsfehler toleriert, jedoch müssen innerhalb weniger Millisekunden wieder korrekte Positionswerte vorliegen. Für eine einwandfreie Motorregelung muss die Verzögerung zwischen dem Einlesen der Position und der Ausgabe der Winkelinformation exakt bekannt sein.

Die Architektur von Resolver-Digital-Wandlern

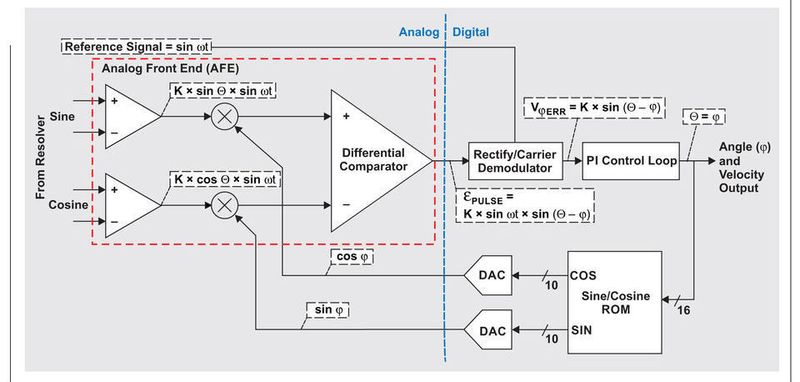
Bild 1 zeigt einen RDC mit einer PLL/VCO-basierten Architektur, der die vom Resolver kommenden analogen Signale in digitale Winkel- und Geschwindigkeitsinformationen umwandelt. Die Winkelinformation ist per Amplitudenmodulation auf die von den Statorwicklungen kommenden Signale aufmoduliert. Diese Signale müssen deshalb demoduliert und aufbereitet werden, um die Winkel- und Geschwindigkeitsinformationen zu extrahieren.

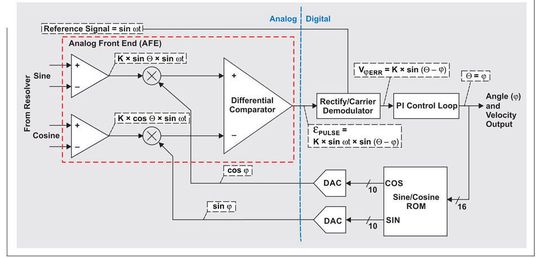
Die RDC-Architektur dient in erster Linie dazu, den Drehwinkel Θ und die Geschwindigkeit (Drehzahl) der Resolver-Welle zu berechnen. Bild 1 veranschaulicht, wie die Winkelstellungs-Information aus der Hüllkurve bzw. den Scheitelspannungen der Sinus- und Cosinussignale am Eingang extrahiert wird.

Modellierung des Systems

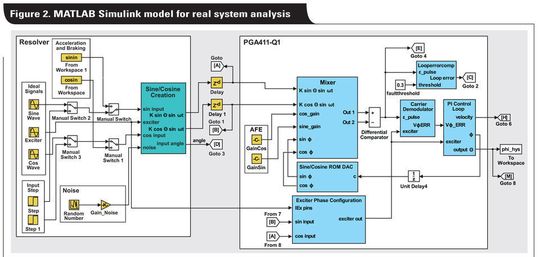
Mit einem auf MATLAB Simulink basierenden Architekturmodell lassen sich mehrere Anwendungsfälle auf der System-Ebene simulieren, wie es in Bild 2 für den PGA411-Q1 erfolgte. Für die Analyse verschiedener Konfigurationen enthält das Systemmodell zwei Hauptabschnitte.

Der in Bild 3 dargestellte Resolver-Eingangsblock unterstützt verschiedene Szenarien des realen Systems, wie zum Beispiel:

1. Statische Winkelmessung

2. Sprungförmige Änderung des Eingangswinkels

3. Individuelle Beschleunigung bzw. Verzögerung

4. Plötzliche Beschleunigung bzw. starkes Bremsen

5. Auswirkungen in das System eingekoppelter Störgrößen

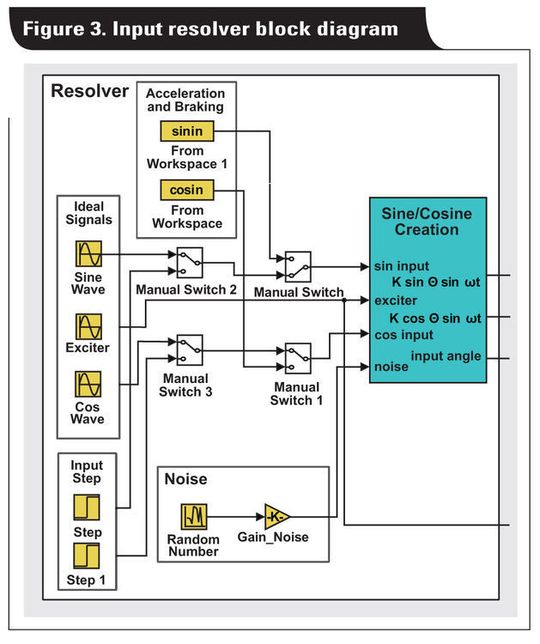
Bei den Ausgängen des Resolver-Blocks handelt es sich um simulierte Signale des Resolver-Sensors.

Sinussignal vom Resolver-Sensor: sin Θ × sin ωt

Cosinussignal vom Resolver-Sensor: cos Θ × sin ωt

Darin steht Θ für den Resolverwinkel und ω für die Frequenz des an die Rotorwicklung R1-R2 gelegten Erregersignals. Die amplitudenmodulierten Signale an der Sinus- und Cosinuswicklung des Resolvers werden innerhalb des Resolver-Blocks erzeugt. Es gibt mehrere Möglichkeiten, Eingangssignale in diesen Block einzuspeisen.

Tabelle 1 zeigt die konfigurierbaren Parameter.

1. Sinus und Cosinus

Sinus: (Frequenz x t) + Phasenwinkel

Frequenz: 2π x fR + (sin_phase × 2π/360) + (Winkel × 2π/360)

Cosinus: (Frequenz x t) + Phasenwinkel

Frequenz: 2π x fR, wobei fR = Drehzahl / 60

Phase: π/2 + Richtung x π + (cos_phase × 2π/360) + (Winkel × 2π/360), wobei fR = Drehzahl / 60

2. Beschleunigen und Bremsen

Spezielle sinin- und cosin-Signale (siehe Bild 3) lassen sich direkt in den Block zur Erzeugung der Sinus- und Cosinussignale einspeisen. Diese Eingangssignale werden nach den Gleichungen 1 und 2 mit dem Erregersignal multipliziert. Ziel ist das Aufstellen eines Daten-Arrays für die Sinus- und Cosinussignale.

Zur Erzeugung der speziellen Signale können die Befehle sin [2π × (fstart × t + 0,5 × accel × t²)] und cos [2π × (fstart × t + 0,5 × accel × t²)] verwendet werden.

3. Sprungantwort

Sprung am Sinuseingang

Anfangswert: sin (Winkel1 x 2π/360)

Endwert: sin (Winkel2 x 2π/360)

Sprung am Cosinuseingang

Anfangswert: sin [π/2 + (Winkel1 × 2π/360)]

Endwert: sin [π/2 + (Winkel2 × 2π/360)]

4. Rauschanalyse

Die Auswirkungen von Rausche auf die Leistungsfähigkeit lassen sich ebenfalls analysieren. So können die mechanischen Vibrationen des Systems ein gewisses Rauschen hervorrufen, das Änderungen des Ausgangswinkels bewirkt. Diese Änderungen müssen auf einen gewissen Bereich eingegrenzt werden (z. B. auf ±0,5°). Weißes Rauschen wird erzeugt und mit einem Faktor K (siehe Bild 3) multipliziert.

(ID:45032600)